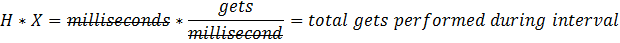Objectives
This post is the first in a series on applying the Universal Scalability Law (USL) to Oracle. It follows up on my March post that applied a Response Time model to Oracle's AWR profiling data. I will show how the same data can be used for both scalability and response time modelling.
Terms like speedup, scalability, response time, and throughput can be confusing. It is also easy to be confused between modelling the number of CPU cores or modelling the number of concurrent users. Since the books referenced below provide the best explanations, my goal is to supplement them with examples, code, data, and commentary. I will provide code in the R programming language, as well as in Mathematica. Performance data will come from a production Oracle database.
Metrics used for modelling performance
Please keep in mind that these examples are just models. They are helpful to the extent that they provide insight, improve predictive abilities, improve monitoring, or provide some other practical benefit. They do not need to be "true" in the strictest possible sense. For example, I have found Oracle's "buffer gets" metric to be a useful measure of throughput. Does this mean throughput is buffer gets? No. It merely means that I have found it useful for a particular application running on particular hardware, experiencing a particular workload. Your model could be quite different and still be useful to you. For example, you might get a better model using Oracle's "user calls" metric. Should we use "buffer gets" or "user calls" to model throughput? There is no one right answer! Simply find a model that works for you. This example code can be easily adapted to your own models.
Universal Scalability Law Overview
The Universal Scalability Law, or "USL," was developed by Dr. Neil Gunther, and is well described in his book Guerrilla Capacity Planning (Springer 2007, chapters 4-6). Craig Shallahamer places the USL into an Oracle context in his book Forecasting Oracle Performance (Apress 2007, chapter 10).
The USL can be thought of as an extension of Amdahl's Law, which concerns speeding up a data processing task through parallelization. Amdahl's Law shows that the serialized parts of the data processing task will limit its speedup, so performance will eventually level off. The USL extends Amdahl's law by accounting for coherency in addition to concurrency. The USL's inclusion of coherency means that performance will actually decrease with excessive parallization, while it merely levels off under Amdahl's Law.
In the previous paragraph, I was intentionally vague with my use of the word paralllelization. Does this term mean adding more CPU processors, or does it mean adding more users? In other words, will the USL predict how many CPUs are needed to support a certain workload, or will it predict how many concurrent users can be supported by an existing software system? The answer: both! Dr. Gunther showed that the USL works for both hardware and software (Gunther 2007, chapter 6).
What about connection pooled OLTP?
As described above, the USL can predict how many concurrent users can be supported by a software system. But what is a "concurrent user" in a connection pooled OLTP web application? A typical web application can support very many concurrent sessions. But from the perspective of the database, most users are inactive most of the time. For any one human user, relatively long times pass between database queries. A common way to architect such applications is to use a pool of database connections. When a user needs to run a query, a database connection is borrowed from the pool, and then returned back to it when the query is finished.
How can we model and measure the "number of concurrent users", N, in such a system?
I show below that the Oracle metric Average Active Sessions (AAS) is equal to N. I describe a simple conceptual model, and apply Little's Law, and derive AAS=N.
A subsequent post will detail a quantitative USL model of production Oracle system, using AWR data, with "buffer gets" as a throughput metric, and using the results from this post, namely that that concurrency N can be modeled with AAS.
Model
A human web user clicks on a link to request a web page. This generates a stream of queries sent to the database; each query takes several logical reads, also known as "buffer gets," or more simply just as "gets."
The variable G is the mean number of "gets" per user click:
Each "get" requires a finite amount of time. The mean response time per "get" in units of milliseconds is the variable R:
The mean response time per click is the product of these two, here symbolized by the variable T:
This model will use observational data from Oracle's Automatic Workload Repository (AWR), which are based on regular snapshots (in this case hourly). I define variable H to be the snapshot duration:
By comparing hourly AWR snapshots of incremental system performance statistics, we can calculate the mean throughput, modeled as buffer gets per unit time. This is variable X:
We can multiply X by H to calculate the total number of gets performed during the snapshot interval:
We can divide that result by G (gets per click) to calculate the total number of user clicks serviced during the snapshot interval.
We can multiply that by T (milliseconds DB response time per click) to get the total amount of database response time during the snapshot interval.
Substituting T = G * R (from above) in the above equation gives the following:
Simplifying gives this:
Dividing both sides of this equation by H gives this:
But we know from Little's Law (see previous post) that this is equal to N, or concurrency:
So we have:
But we also know that this is the definition of Oracle's Average Active Session (AAS) metric
Finally, equating these two gives us an equivalency of concurrency and AAS:
The mean response time per click is the product of these two, here symbolized by the variable T:
This model will use observational data from Oracle's Automatic Workload Repository (AWR), which are based on regular snapshots (in this case hourly). I define variable H to be the snapshot duration:
We can multiply X by H to calculate the total number of gets performed during the snapshot interval:
We can divide that result by G (gets per click) to calculate the total number of user clicks serviced during the snapshot interval.
We can multiply that by T (milliseconds DB response time per click) to get the total amount of database response time during the snapshot interval.
Substituting T = G * R (from above) in the above equation gives the following:
Simplifying gives this:
Dividing both sides of this equation by H gives this:
But we know from Little's Law (see previous post) that this is equal to N, or concurrency:
So we have:
But we also know that this is the definition of Oracle's Average Active Session (AAS) metric
Finally, equating these two gives us an equivalency of concurrency and AAS: