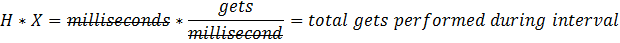Universal Scalability Law (USL) in an Oracle OLTP database

Introduction

This post is the second in a series on applying the Universal Scalability Law (USL) to Oracle OLTP. It follows up on my July post that gave an overview of the USL, and showed how Oracle "Average Active Sessions" (AAS) metric could be used to model concurrency "N".

The goal here is to estimate seriality and coherency parameters, Αlpha and Βeta respectively, that can be used to predict OLTP throughput as a function of concurrency "N". This is achieved by fitting the USL to observations of Oracle performance metrics that are easily queried from the Automatic Workload Repository (AWR). This model can be used for capacity planning and to set realistic monitoring targets. It also provides insight into the relative importance of serialization and coherency limits to system throughput. 

The USL was developed by Dr. Neil Gunther, and is well described in his book Guerrilla Capacity Planning (Springer 2007, chapters 4-6). Craig Shallahamer places the USL into an Oracle context in his book Forecasting Oracle Performance (Apress 2007, chapter 10). The USL can be thought of as an extension of Amdahl's Law, which concerns speeding up a data processing task through parallelization. Amdahl's Law shows that the serialized parts of the data processing task will limit its speedup, so performance will eventually level off. The USL extends Amdahl's law by accounting for coherency in addition to concurrency. The USL's inclusion of coherency means that performance will actually decrease with excessive parallization, while it merely levels off under Amdahl's Law.

In the previous paragraph, I was intentionally vague with my use of the word paralllelization. Does this term mean adding more CPU processors, or does it mean adding more users? In other words, will the USL predict how many CPUs are needed to support a certain workload, or will it predict how many concurrent users can be supported by an existing software system? The answer: both! Dr. Gunther showed that the USL works for both hardware and software (Gunther 2007, chapter 6).

This post is divided into these sections:

• USL model detailed description
• Observations from a production database
• Estimate throughput at N = 1
• Normalize throughput observations to convert to capacityRatio
• Fit USL model to observations to estimate parameters Alpha and Beta

I implemented this model in Mathematica, and my notebook and data are available for download, along with a PDF version of the notebook. A later post will show how to implement this mode in the open source R programming language.

USL model detailed description

Define N as concurrency, the number of concurrent "users." Here it is modelled as Oracle "Average Active Sessions" (AAS), as explained in my July post.

Define X as throughput. Here it is modeled as Oracle "buffer gets" per millisecond as a function of N, and given the variable name throughPut (Gunther 2007 p. 52 eq. 4.20 as modified by p. 101 Section 6.3). Note that you are free to model your database using whichever throughput metrics are most appropriate. For example, many of Shallahamer's example use the Oracle metric "user calls." No single correct throughput metric exists, so you might want to experiment with several to see which has the best predictive ability.


throughPut = X(N)

Then X(1) is the throughput where N=1 (Ibid.). It is obviously not possible to set N=1 in a production Oracle database when using this N=AAS model, since AAS is estimated through observation rather than set to arbitrary values. The variable name throughPutOne is used here for X(1) and its value is estimated by linear regression as shown below.

throughPutOne = X(1)

Define C(N) as the "capacity ratio" or "relative capacity" as the ratio of X(N) to X(1) at a given value of N (Gunther 2007 p. 77). The variable capacityRatio is used here for C(N).

capacityRatio = C(N) = X(N)/X(1)

Gunther's Universal Scalability Law (USL) as modified for software scalability is shown below. (Gunther 2007 p. 101 eq. 6.7). The variable n is used here for N. A goal of this study is to estimate parameters Alpha and Beta, which characterize seriality and coherency respectively.

capacityRatio = n / (1 + Alpha (n - 1) + Beta n (n - 1))

Here is how Mathematica displays and simplifies this formula:

Observations from a production database

I obtained Oracle performance metric data observations from an AWR query on a production system. This query is heavily documented, so see the SQL text for details. It uses both "subquery factoring" (aka "common table expressions" and lead() analytic function.

This query calculates deltas of hourly snapshots of several Oracle resource usage counters (see this article for more about AWR).  For this USL model, we need only these two columns:

• DB_TIME_CSPH = centiseconds of "DB Time" used in one hour. As explained here, "DB time" is the sum of time spent on the CPU and in "active" waits
• BUFFER_GETS_PH = buffer gets done in one hour, a measure of throughput.

See the notebook or PDF for details about importing these query results into Mathematica. One of the trickiest parts is converting to the correct units of measure, which always seems trickier than it should!

Estimate throughput at N = 1

As mentioned above, it is obviously not possible to set N=1 in a production Oracle database when using this N=AAS model, since AAS is estimated through observation rather than set to arbitrary values. We will use linear regression on this subset to estimate the throughput at AAS=1.

I used the subset of observations where AAS was less than 1.5. This estimated throughput at AAS=1 is needed to normalize throughput observations to unitless capacityRatio.


See the notebook or PDF for details about doing the linear regression with Mathematica. I show below the regression line along with the subset of observations. I estimate throughPutOne = X(1) = 101.62 buffer gets per millisecond at AAS=1.

Normalize throughput observations to convert to capacityRatio

I show below how to normalize throughput observations to convert to capacityRatio = C(N) = X(N)/X(1).

I include a sanity check and plot.

Fit USL model to observations to estimate parameters Alpha and Beta


I use Mathematica's  FindFit[data,expr,pars,vars] to estimate parameters Alpha and Beta, which characterize seriality and coherency respectively. The capacity ratio form of the USL is repeated below. (Gunther 2007 p. 101 eq. 6.7). The variable n is used here for N and is the first column in the nCapacityRatio (nested list) table and can be thought if as the independent variable. The second column of data, the normalized capacity ratio from immediately above, is considered to be the observed value of the capacityRatio formula.

capacityRatio = n / (1 + Alpha (n - 1) + Beta n (n - 1))

I prepare the USL model by substituting best fit parameters and simplifying.

Finally, I plot USL model along with the normalized observations. This model well predicted system throughput, and helped to fine tune production monitoring and troubleshooting protocols.

Downloads

• Mathematica notebook and data
• A PDF version of the notebook

Concurrency of a connection pooled OLTP database: N=AAS

Objectives


This post is the first in a series on applying the Universal Scalability Law (USL) to Oracle. It follows up on my March post that applied a Response Time model to Oracle's AWR profiling data. I will show how the same data can be used for both scalability and response time modelling.

Terms like speedup, scalability, response time, and throughput can be confusing. It is also easy to be confused between modelling the number of CPU cores or modelling the number of concurrent users. Since the books referenced below provide the best explanations, my goal is to supplement them with examples, code, data, and commentary. I will provide code in the R programming language, as well as in Mathematica. Performance data will come from a production Oracle database.

Metrics used for modelling performance

Please keep in mind that these examples are just models. They are helpful to the extent that they provide insight, improve predictive abilities, improve monitoring, or provide some other practical benefit. They do not need to be "true" in the strictest possible sense. For example, I have found Oracle's "buffer gets" metric to be a useful measure of throughput. Does this mean throughput is buffer gets? No. It merely means that I have found it useful for a particular application running on particular hardware, experiencing a particular workload. Your model could be quite different and still be useful to you. For example, you might get a better model using Oracle's "user calls" metric. Should we use "buffer gets" or "user calls" to model throughput? There is no one right answer! Simply find a model that works for you. This example code can be easily adapted to your own models.


Universal Scalability Law Overview

The Universal Scalability Law, or "USL," was developed by Dr. Neil Gunther, and is well described in his book Guerrilla Capacity Planning (Springer 2007, chapters 4-6). Craig Shallahamer places the USL into an Oracle context in his book Forecasting Oracle Performance (Apress 2007, chapter 10).

The USL can be thought of as an extension of Amdahl's Law, which concerns speeding up a data processing task through parallelization. Amdahl's Law shows that the serialized parts of the data processing task will limit its speedup, so performance will eventually level off. The USL extends Amdahl's law by accounting for coherency in addition to concurrency. The USL's inclusion of coherency means that performance will actually decrease with excessive parallization, while it merely levels off under Amdahl's Law.

In the previous paragraph, I was intentionally vague with my use of the word paralllelization. Does this term mean adding more CPU processors, or does it mean adding more users? In other words, will the USL predict how many CPUs are needed to support a certain workload, or will it predict how many concurrent users can be supported by an existing software system? The answer: both! Dr. Gunther showed that the USL works for both hardware and software (Gunther 2007, chapter 6).

What about connection pooled OLTP?

As described above, the USL can predict how many concurrent users can be supported by a software system. But what is a "concurrent user" in a connection pooled OLTP web application? A typical web application can support very many concurrent sessions. But from the perspective of the database, most users are inactive most of the time. For any one human user, relatively long times pass between database queries. A common way to architect such applications is to use a pool of database connections. When a user needs to run a query, a database connection is borrowed from the pool, and then returned back to it when the query is finished.

How can we model and measure the "number of concurrent users", N, in such a system?

I show below that the Oracle metric Average Active Sessions (AAS) is equal to N. I describe a simple conceptual model, and apply Little's Law, and derive AAS=N.

A subsequent post will detail a quantitative USL model of production Oracle system, using AWR data, with "buffer gets" as a throughput metric, and using the results from this post, namely that that concurrency N can be modeled with AAS.

Model

A human web user clicks on a link to request a web page. This generates a stream of queries sent to the database; each query takes several logical reads, also known as "buffer gets," or more simply just as "gets."

The variable G is the mean number of "gets" per user click:

Each "get" requires a finite amount of time. The mean response time per "get" in units of milliseconds is the variable R:

The mean response time per click is the product of these two, here symbolized by the variable T:

This model will use observational data from Oracle's Automatic Workload Repository (AWR), which are based on regular snapshots (in this case hourly). I define variable H to be the snapshot duration:

By comparing hourly AWR snapshots of incremental system performance statistics, we can calculate the mean throughput, modeled as buffer gets per unit time. This is variable X:

We can multiply X by H to calculate the total number of gets performed during the snapshot interval:

We can divide that result by G (gets per click) to calculate the total number of user clicks serviced during the snapshot interval.

We can multiply that by T (milliseconds DB response time per click) to get the total amount of database response time during the snapshot interval.

Substituting T = G * R (from above) in the above equation gives the following:

Simplifying gives this:

Dividing both sides of this equation by H gives this:

But we know from Little's Law (see previous post) that this is equal to N, or concurrency:

So we have:

But we also know that this is the definition of Oracle's Average Active Session (AAS) metric

Finally, equating these two gives us an equivalency of concurrency and AAS:

Little's Law example: Oracle shared pool

Objective

This post illustrates Little's Law using example data from a production Oracle system. The goal is to demonstrate how easy it is to use and interpret. In fact, it is so easy that it seems more like intuition than a Law, and is easy to overlook its usefulness.

Little's Law

Little's Law expresses a simple relationship between request arrival rate, residence time and the number of requests either in service or in a queue. Whenever you know two of these quantities, Little's Law allows you to calculate the third one.  Little's Law only holds for averages in a stable system.

Little's Law is intuitive and easy to understand. It can be applied to many situations, and provides an easy and powerful sanity check for many database performance metrics. To illustrate this law, I show an example using Oracle's shared pool and query hard parse rate.

For more information, see Dr. Neil Gunther's The Practical Performance Analyst (Author's Choice Press 2000, p. 44)  or Craig Shallahamers's Forecasting Oracle Performance (Apress 2007, p. 99).

The long-term average number of customers in a stable system L is equal to the long-term average arrival rate, λ, multiplied by the long-term average time a customer spends in the system, W, or:

L = λW

Oracle shared pool

Remember that an Oracle hard parse converts a string of SQL text into a new executable cursor and puts it into the cache of cursors in the shared pool. Consider the following substitutions to Little's Law above as we apply it to cursors in the Oracle shared pool.

Little's Law	Oracle
customer	cursor
system	shared pool
long-term average number of customers in a stable system L	number of cursors already in the shared pool plus those getting hard parsed right now
long-term average arrival rate, λ	hard parse rate
long-term average time a customer spends in the system, W	average cursor retention time in shared pool

We can ignore the number of cursors "getting hard parsed right now" since that number will be so much smaller than the number of cursors already in the shared pool. With this simplification, Little's Law when applied to Oracle hard parsing becomes the following:

The average number of cursors in the shared pool is equal to the average hard parse rate multiplied by the average time a cursor spends in the shared pool.

Assume that we want to estimate the average retention time of a parsed SQL statement in the shared pool. Oracle's instrumentation makes it easy to measure both the rate of hard parsing and the count of cursors in the shared pool.

If we rearrange Little's Law, we get:

W = L/λ

which means that:

mean retention time in shared pool = (number of cursors in the shared pool)/(hard parse rate)

Using values of 5,000 cursors (rows in V$SQL) and 100 hard parses per second, we get

mean retention time in shared pool = (5000)/(100 hard parses per second)

mean retention time in shared pool = 50 seconds

Q-Q plots to examine SQL execution time distributions

Introduction

The purpose of this post is to introduce the use of Q-Q plots for comparing distributions of sampled observational data to standard, reference distributions. For example, we often assume that our sampled observations are normally distributed. A Q-Q plot can quickly show whether this assumption is justified. A Q-Q plot can be used with other distributions beside normal. For example, both log-normal and Poisson distributions are demonstrated below. I also show an estimated density plot, which is similar to a histogram, but is "more robust and easier to read" (R in a Nutshell, Joseph Adler, O'Reilly Media 2009, p.238).

Performance data gathered from a production Oracle database are used to illustrate the technique. Since these data fit none of these standard distributions, the Q-Q plots all look rather strange. To illustrate a Q-Q plot for a good fit, I generate random log-normal data, and compare them to normal and log normal distributions.

A secondary purpose of this post is to show how Q-Q plots can be generated quickly and easily using the R programming language, which is free and open source. The R programming language has become the lingua franca of data science and statistics.

The data and R code I used for this analysis are available for download (links below).

Q-Q Plot Overview

The "Q" in Q-Q plot comes from "quantile." You are already familiar with quantiles if you understand medians, quartiles, and percentiles. Assume you have a large set of X values. The median is the specific value of X where half of the other values are less that the median value, and half are greater. Quartiles are similar: three-fourths of the X values are less than the third quartile. Of course, percentiles are the same: only ten percent of the students score greater that the 90th percentile.

The term "quantile" simply generalizes this concept to an arbitrary number of partitions, rather than just two,four, or one hundred partitions assumed by medians, quartiles, and percentiles.

To generate a Q-Q plot, you first divide the sampled observational data into k quantiles. To compare these to a known, reference distribution, you also divide it into k quantiles. You then work your way through each value of k, plotting each quantile value of the observational data as the x-coordinate, and the corresponding reference distribution quantile as the y-coordinate. 

Bottom line: If the distributions are the same, you will end up with a straight line. Deviations from a straight line suggest differences between the sampled and reference distributions. 

A common practice is to standardize each dataset by subtracting its mean and dividing by its standard deviations (i.e., "z score"). With this transformation, the straight line would have a slope of one and pass through the origin; this standardization can simplify the plot.

Much more thorough discussion, and more complete advice on distributional analysis in R is available at the following links. If you really want to learn this stuff, you should read these sources and not this blog!

• Bill Huber: http://www.quantdec.com/envstats/misc/Fitting data to distributions.pdf
• Vito Ricci: http://cran.r-project.org/doc/contrib/Ricci-distributions-en.pdf

as linked from here:

• http://www.statmethods.net/advgraphs/probability.html

In the R programming language, Q-Q plots are prepared using functions like qqplot() and qqnorm(). In Mathematica, they are prepared using QuantilePlot[]

Data source

Earlier this year, Craig Shallahamer blogged about distributions of elapsed times of SQL query executions in the Oracle Database:

• http://shallahamer-orapub.blogspot.com/2011/02/sql-statement-elapsed-times.html
• http://shallahamer-orapub.blogspot.com/2011/02/sql-arrival-patterns-and-impact.html
• http://shallahamer-orapub.blogspot.com/2011/02/important-statistical.html

Craig noted the difficulty of comparing distributions by visually examining histograms: "Just because a data set visually looks very much like another data set or statistical distribution, does not mean it statistically matches...be careful." I completely agree, and my goal here is to show how distribution differences are much easier to see with Q-Q plots that they are with histograms.

For the analysis below, I used one of Craig's datasets, which he refers to as "Garr 8q"and it is in file Garret8qtkxy0g5d1p3_1.txt within his AnalysisPack.zip, I have have included a copy of these data for download. Here is Craig's histogram:

Unusual distributions common in Oracle database studies

As a side note, many data distributions observed in Oracle database performance studies are highly skewed or bimodal, obviously not normally distributed. In fact, most of the interesting Oracle database performance problems I encounter are in large part caused by strange distributions. Weird distributions are a fact of life for the database professional. I chose this particular dataset since it was less pathological than the others in Craig's study. 

By the way, I am ignoring here the basic question: why should I care about the distribution of SQL query execution times? See Craig's posts for his discussion on this topic. Bill Huber addresses this general question in detail in his PDF presentation.

Results - actual database performance data

I encourage you to look at the R source code to see how easy it is to do this type of analysis. However, I will not include this code within the text of this post.

Craig concluded that his example SQL query execution elapsed time data did not seem to be coming from normal, log-normal, or Poisson distributions. I agree. Let's first look at the estimated density function,which is similar to a histogram.

The next plot (below) is a normal Q-Q plot. We want to graphically compare the sample quantiles to the expected quantiles. If samples were taken from a normal distribution, the points would line up with a slope of 1 and and intercept of zero. Significant deviations from this line indicate a lack of fit to the normal distribution. We see significant deviations below, so we discard the notion that the samples came from a normal distribution. 

Lets try a log transform of these data to see if they came from a log-normal distribution . We again see significant deviations from a straight line (below), so these data were not sampled from a log-normal distribution.

We now compare the Oracle SQL elapsed time data to a randomly generated Poisson distribution. Once again, we see significant deviations from the line, so we conclude that the observations were not sampled from a Poisson distribution.

Results - randomly generated data

The above Q-Q plots are so completely different from straight line good fits. So let's see a Q-Q plot for a good fit. I generated some random log-normal data to illustrate a good fit, and here is what the distribution looks like.

But first, let's compare these random log-normal data to a normal distribution.  Again, not a good fit, as expected:

Now let's take the log() of the  random log-normal data and compare the transformed data to a normal distribution. This is the near perfect fit we expect.

Conclusions

I have demonstrated the use of Q-Q plots to compare the distribution of sampled observations to known distributions. Deviations between sample data distributions and three reference distributions were obvious. The deviations were easier to see in a Q-Q plot that in histograms. Q-Q plots can be generated quickly and easily using the R programming language, which is free and open source. 

Code and data

• Actual data, R source code only: Garret8q.QQ-plot.R.txt
• Actual data, R source, data, and output: Garret8q.QQ-plot.tar
• Random log normal data, R source code only: log-normal.QQ-plot.R.txt
• Random log normal data, R source and output: log-normal.QQ-plot.tar

My first issue of the NoCOUG Journal as Editor

I am thrilled and honored to take over the reins of the NoCOUG Journal! 

My first issue as Editor was just published and can be downloaded from the NoCOUG website at http://www.nocoug.org/Journal/NoCOUG_Journal_201105.pdf. It kicks off a new series of short articles called "Ask the Oracle ACEs" where you can read diverse advice from several experts in response to a single question. The question for this issue was intentionally vague: "Why is my database slow?" This issue also continues regular features such as an interviews and book reviews. For this May 2011 issue, our interview is with Greg Rahn, a database performance engineer in the Real-World Performance group at Oracle Corporation, and Brian Hitchcock reviews the new book "Achieving Extreme Performance with Oracle Exadata" by Rick Greenwald, et al.

I especially want to thank Iggy Fernandez who has been the editor for the last five years. He set very high standards, and I'll be working very hard to follow in his footsteps. NoCOUG's speakers, authors, and vendors have given us all a tremendous amount of practical skills and real-world advice for the last 25 years. Their generosity and commitment have benefited us all. Even the end users of our databases are happier because of the skills that have been passed on to us! I am convinced that sharing and collaboration are the keys to professional growth and success. With this inspiration in mind, I'll do my best to ensure that this Journal continues to be a vital source of knowledge.

Also, the NoCOUG spring conference is this Thursday, May 19 at the Oracle Corporation in Redwood Shores. See the agenda at http://nocoug.org/next.html. Presentation materials will be available for download at http://www.nocoug.org/presentations.html.

Referential integrity and optimizer shortcuts

I overheard again just the other day that database performance can be improved by eliminating foreign keys and doing integrity constraint checking in the application. This fallacy is based on the notion that there must be some database overhead for enforcing foreign key constraints, so the database will always be faster if it can avoid this overhead. In fact, Oracle's foreign key implementation is very efficient, and in real world cases, the overhead of foreign keys is negligible, and can sometimes even provide slightly faster DML (see, for example, Tom Kyte).

Moreover, referential integrity can provide huge performance gains in situations where Oracle's optimizer can use it to devise better execution plans. I stumbled upon an example of this recently in a production system and thought I'd share it.

The query below involves five tables related by foreign keys. The joins follow these foreign keys.

select count(*)
 from goats g,
      properties p,
      doelings d,
      goat_versions v,
      farm_animals f
where g.type_id = :1
  and g.property_id = p.property_id
  and g.goat_id = d.doeling_id
  and d.status = 'alive'
  and g.goat_id = v.alive_id
  and f.animal_id = g.goat_id
;

The execution plan with predicates is shown below. In this farm animal database, index names start with their table name prefix. Please do not spend too much time studying this plan; I'll walk you through the important parts below.

-----------------------------------------------------------------------
| ID  | OPERATION                       | NAME                        |
-----------------------------------------------------------------------
|   1 |  SORT AGGREGATE                 |                             |
|   2 |   NESTED LOOPS                  |                             |
|   3 |    NESTED LOOPS                 |                             |
|   4 |     NESTED LOOPS                |                             |
|*  5 |      TABLE ACCESS BY INDEX ROWID| GOATS                       |
|*  6 |       INDEX RANGE SCAN          | GOATS_TYPE_IDX              |
|*  7 |      INDEX UNIQUE SCAN          | GOAT_VERSIONS_ALIVE_ID_UNIQ |
|*  8 |     INDEX UNIQUE SCAN           | FARM_ANIMALS_PK             |
|*  9 |    TABLE ACCESS BY INDEX ROWID  | DOELINGS                    |
|* 10 |     INDEX UNIQUE SCAN           | DOELINGS_DOELING_ID_PK      |
-----------------------------------------------------------------------

PREDICATE INFORMATION (IDENTIFIED BY OPERATION ID):
---------------------------------------------------

   5 - FILTER("G"."PROPERTY_ID" IS NOT NULL)
   6 - ACCESS("G"."TYPE_ID"=:1)
   7 - ACCESS("G"."GOAT_ID"="V"."ALIVE_ID")
       FILTER("V"."ALIVE_ID" IS NOT NULL)
   8 - ACCESS("G"."GOAT_ID"="F"."ANIMAL_ID")
   9 - filter("D"."STATUS"='alive')
  10 - ACCESS("G"."GOAT_ID"="D"."DOELING_ID")

First, notice how the PROPERTIES table (P) is not accessed, nor or any of its indexes! Second, notice how the predicate for operation #5 (g.property_id is not null) is not in the original SQL above; the Oracle optimizer added it on its own!

What is going on?

The Oracle optimizer knows that the PROPERTY_ID column in child table GOATS (G) is a foreign key to parent table PROPERTIES (P). The query SQL text includes the join condition "G.PROPERTY_ID = P.PROPERTY_ID." But due to referential integrity, all values of G.PROPERTY_ID must also exist in P.PROPERTY_ID. Therefore, if G.PROPERTY_ID is not null, then this join condition must be satisfied.

The Oracle optimizer has used this knowledge to eliminate the need to access parent table PROPERTIES (P) or any of its indexes. This provides a significant cost savings. This shortcut would not have been available if referential integrity had been enforced by the application.

A small data mining library

In my quest to learn data mining, I have studied others' book reviews in order to assemble a small data mining library. I share the results of this quest in this blog post. I've already finished reading some of these books, am studying others, and will probably never finish some of them. Enjoy!

This list is divided into several sections: 

• R
• Data Mining
• Regression, ANOVA, and Statistics
• Applications

R

R in a Nutshell (Joseph Adler. O'Reilly 2010). A basic, general introduction to the R language. It is comprehensive, but necessarily thin in spots. For example, it devotes over one hundred pages to graphics, but less than a page to support vector machines. Those new to R should probably start with this book.

Data Manipulation with R (Phil Spector. Springer 2008). One the beautiful things about R is how it handles datasets. This book explains all that you need to know about "data frames", and goes into detail about how to use "factors," how to access databases, etc. We often spend more time managing data than analyzing it, and this book show you how to use R effectively. I especially like the lessons on R's "melt" and "cast" functions: they let you "denormalize" data, like you can now do with Oracle 11g's pivot() function.

Modern Applied Statistics with S (W.N. Venables, B.D. Ripley. Springer 2010). This essential book focuses on practical use of R to analyze data. It includes some statistical theory, but only just enough to provide context and clarity. It emphasizes practical examples, and has a very wide scope.

Statistical Models in S (J. M. Chambers, T.J. Hastie. Chapman and Hall/CRC 1991) This reference book on statistical modeling goes into much more implementation detail that Venables and Ripley (above). It provides a firm foundation for understanding R functions and models.

Data Mining

All of Statistics: A Concise Course in Statistical Inference (Larry Wasserman. Springer 2010). This book provides a crash course on statistics. It starts with a basic definition of probability, where the basic problem is "given a data generating process, what are the properties of the outcomes?" contrasted with inference: "given a set of outcomes, what can we say about the process that generated the data?" It provides a firm mathematical foundation: for example it clearly defines samples spaces, random variables, cumulative distribution functions (CDF), and probability density functions (PDF). The reader is assumed to be very comfortable with calculus and linear algebra, and is expected to follow proofs of its many theorems. Bibliographic notes are provided, as well as homework exercises.

The Elements of Statistical Learning: Data Mining, Inference, and Prediction (Trevor Hastie, Robert Tibshirani and Jerome Friedman. Springer 2009). A complete guide to data mining techniques, with eighteen chapters and seven hundred pages. The first several chapters are considered essential, while the rest can be read independently. It includes computational considerations and extensive bibliographies. Used as the textbook for Machine Learning 201 and 202 taught at the Hacker Dojo.

Data Mining: Practical Machine Learning Tools and Techniques (Ian Witten. Morgan Kaufmann 2011). A basic introduction to data mining. It uses Weka rather than R.

Introduction to Data Mining (Pang-Ning Tan, Michael Steinbach, Vipin Kumar. Addison Wesley 2005). A very accessible, yet comprehensive introduction to data mining. It requires only a minimal mathematical background, and includes data pre- and post-processing. Used as the textbook for Machine Learning 101 and 102 taught at the Hacker Dojo.

Regression, ANOVA, Statistics

Applying Regression and Correlation: A Guide for Students and Researchers (Dr. Jeremy Miles, Dr. Mark Shevlin. Sage 2000). A lovely introduction to regression, targeted to the non-mathematician. I enjoy how it starts by showing how the mean is a least-squares model: the mean minimizes the sum of squared residuals. Starting with the mean and progressing to simple linear regression makes it easier to understand multiple regression. This approach also makes it easier to see analysis of variance (ANOVA) as a form of regression.

Nonlinear Regression with R (Christian Ritz, Jens Carl Streibig. Springer 2008). This book focuses on nonlinear regression, going into deep practical detail about the R functions nls() and model diagnostics. It is not a book on theory. It is designed for self study for those familiar with, but not yet experts in regression and R.

Statistical Methods, 8th Edition (George Snedecor, William Cochran. Iowa State University Press 1989). A classic, covering the basics from a very practical perspective.

Analysis of Variance (Henry Scheffé. Wiley 1959). A complete mathematical foundation for the analysis of variance; another classic. It assumed the reader is comfortable with calculus and linear algebra. It is designed for self-study.

Applications

Profiles in Performance: Business Intelligence Journeys and the Roadmap for Change (Howard Dresner, Wiley 2009). While not a book on data mining per se, it outlines the organizational issues necessary for success with business intelligence technologies. He defines four levels of organizational maturity as measured by six "performance-directed culture criteria." These include "transparency and accountability", and "availability and currency of information." The book is based on very detailed, insightful, and inspiring case studies.

Smart Enough Systems: How to Deliver Competitive Advantage by Automating Hidden Decisions

(James Taylor, Neil Raden. Prentice Hall 2007), This book focuses on the small descions made every day by an organization, such as those made by front-line customer service representatives. While each of these decissins may be very small, their cumulative effect is greater than the strategic descions that get most upper management attention. The author advocates for "enterprise decision management" to optimize precision, consistency, agility, and speed of these routine operational decisions. This can be accomplished by making suitable predictive models easily available and automatic.

PMML in Action (Alex Guazzelli, Wen-Ching Lin, Tridivesh Jena. CreateSpace 2010), The Predictive Model Markup Language (PMML) is an industry standard way of sharing predictive models between software applications. This book provides very practical advice for using and understanding PMML illustrated with thorough examples.

Response time analysis based on AWR data

Summary

The basic idea here was to do a database CPU response time analysis using a whole month's worth of hourly observations of a busy production system. Craig Shallahamer provides an online tool that does a curve-fit of a single observation to the basic response time formula (http://filezone.orapub.com/cgi-bin/msolve.cgi). However, it seems like a better model might be obtained if one could do the curve-fitting with hundreds of observations. For fun, I did the analysis twice: once in using R (http://www.r-project.org/), and once using Mathematica (http://www.wolfram.com/); source code and example data for each program are available for download below. I developed an excellent response time model, and had a few other insights:

• Observational periods where the CPU utilization is much higher than predicted by a linear regression of utilization versus workload (i.e., outliers) are very interesting from a trouble shooting perspective. This suggests the possibility of monitoring for such outliers.
• Observational periods where the response time is much higher than predicted based on comparable workload are very interesting from a trouble shooting perspective. Again, this suggests the possibility of monitoring for such outliers.

Data source, metrics, and model

I used hourly snapshots of V$SYSSTAT data: foreground CPU utilization, DB time, buffer gets and user calls. I gathered these data for daytime, weekdays only, one a busy OLTP-like production system. I computed deltas for each metric, so these deltas represent hourly averages. I could have written my own tool to gather these data, but found it more convenient to simply use AWR's snapshots. My query is available for download (below); it uses subquery factoring for easy review and maintenance, the analytic function LEAD() to compute deltas without a self-join, and the max-decode denormalization trick.

I modeled this 4-CPU Oracle database as follows:

• workload = buffer gets per millisecond
• service time = milliseconds of foreground CPU per buffer get
• response time = millisecond of DB time per buffer get

Utilization as function of workload

We expect CPU utilization to be a linear function of workload (Gunther 1998/2000 p. 51, Shallahamer 2007 p. 26, Shallahamer 2010 p. 51). As shown below most of the observations fit very well to a linear regression. Yet we do have some apparent outliers, above and to the right.

Outliers - linear model - practical diagnostic value

Although the above scatter plot visually suggests the presence of outliers, it would be nice to have an objective, quantitative approach to identifying them. A common solution is to use a histogram of the residuals (Miles 2009 p. 88, http://www.jeremymiles.co.uk/regressionbook/extras/appendix2/R/).

The outliers are over on the right side of the histogram, with residuals above about 8 or so. The remaining residuals have a nice, normal-like distribution, as expected.

One of the beautiful and convenient features of the R language is the ability to easily combine regression residuals with the raw data, which allows them to be easily managed and reviewed. These steps were much more cumbersome in Mathematica or Excel. My R source code, available for download below, demonstrates this technique in detail. Here is how this was done with a single R command:

db9.c.cleaned <- subset( cbind(db9.b.milliseconds, residuals(db9.b.milliseconds.lm)),

                         residuals(db9.b.milliseconds.lm) < 8.0 )

I want to emphasize that I did not simply remove these outliers so that the rest of the analysis would have prettier, better fitting lines. Instead, these outliers were important from a diagnostic and database management perspective. A review of database activity during the hours represented by the outliers revealed that bulk operations intended to run at night were mistakenly running during business hours. These bulk operations required more CPU time per buffer get than typical for business hour activity. The reason for this difference was not investigated in detail, yet this regression analysis brought it to our attention so we can now manage it. This insight had escaped identification via routine database monitoring. This discovery opens up new ways of monitoring database health!

Not shown here, but available for download, are the regression model, plots, and residual histograms after removal of outliers. As you can imagine, the regression was quite tight: R-squared was 0.945, and the residual histogram was very normal looking.

Response and service time scatter plot

I show below a scatter plot of response time (i.e., circles, DB time) and service time (i.e., crosses, foreground CPU time) as a function of workload (i.e., buffer gets per millisecond), after removal of the above outliers. 

As expected, the service time was nearly constant with workload. This constancy of service time is related to the linear relationship between CPU utilization and workload. If service time per buffer get was not constant, then we would not expect utilization to be linear.

This plot also shows apparent response time outliers, hours with much more wait time than the workload would suggest. As with the utilization outliers above, I objectively identified them by reviewing a histogram of residuals from a regression (although I cheated by using a linear rather than non-linear regression, details in downloadable source code). And as with the utilization outliers above, these had significant diagnostic value. We had occasional trouble with excessive non-idle waits that stand out much more dramatically and obviously than with conventional database monitoring. Again, this discovery opens up yet another potential new way of monitoring database health!

Response time model - nonlinear regression

This database system can be modeled as a single queue (i.e., the CPU run queue) with multiple "servers" (i.e., CPUs).  An approximate formula for this model is shown below (Gunther 1998/2000 p. 62, equation 2-36, Shallahamer 2007 p. 26, Shallahamer 2010 p. 51).

I was able to simplify this model further, by assuming a constant value of service time, using its average value of 0.009295 milliseconds per buffer get. My goal was to solve for the number of effective "servers" on this 4-CPU database host. I gave this formula to R's nonlinear regression function as shown below (download source code to see in it context).

db9.f.cleaned.nls <- nls(DB_TIME_MSPMS/BUFFER_GETS_PMS~0.009295/(1-(((0.009295*BUFFER_GETS_PMS)/num.servers)^num.servers)),

   data = db9.f.cleaned,

   start=list(num.servers=2.5),

   trace=TRUE)

Results and conclusion

A plot of the fitted model is shown below; a pretty good fit was obtained. As you can see, this system was often running pretty close to the "knee in the curve." Little excess CPU capacity was available, and a CPU upgrade was in order (SQL tuning and workload reduction techniques had already been exhausted). 

Regarding CPU upgrades, a question naturally arises: is it better to add more CPUs, or to increase the speed of the CPUs? The following Mathematica plot compares these two alternatives, assuming that we can either double the number of (effective) CPUs or double their speed (i.e., halve their service time).

Now that the CPUs have been upgraded on this host, a future blog post will compare these predictions to post-upgrade observations. Future posts will also describe the results of practical database monitoring based on finding regression model outliers. 

Downloads

AWR SQL only (txt)

R source code only (txt)

R source code, plots, SQL, and data (zip)

Mathematica notebook and data (zip)

Mathematica PDF (pdf)

References

Gunther, N. J. (1998, 2000). The Practical Performance Expert. Lincoln, NE: Author's Chioce Press (originally published by McGraw Hill).

Miles, J and Shevlin S. (2001, ... 2009). Applying Regression and Correlation. London, Thousand Oaks CA: SAGE publications. See also http://www.jeremymiles.co.uk/regressionbook/extras/appendix2/R/

Shallahamer, C. (2007). Forecasting Oracle Performance. Berkeley, CA: Apress (distributed by Springer-Verlag).

Shallahamer, C. (2010). Orapub's 2020 Performance Seminar, Northern California Oracle Users' Group (NoCOUG) Training Day, August 18 2010.

Institute of Arctic Biology at the University of Alaska Fairbanks. R tutorial, especially non-linear regression: http://mercury.bio.uaf.edu/mercury/R/R.html#nonlinear